Lecture 2 : Berry Phase and Chern number¶

Berry Phase review¶

Assuming a physical system is depended on some parameters \(\mathbf{R}=(R_1,R_2,\cdots,R_N)\), we have the snapshot Hamiltonian \(H(\mathbf{R})\), its eigen-values and eigen-states:

\[H(\mathbf{R})|n(\mathbf{R})\rangle=E_n(\mathbf{R})|n(\mathbf{R})\rangle\]

where \(|n(\mathbf{R})\rangle\) can have an arbitrary phase prefactor.

The parameters \(\mathbf{R(t)}\) are slowly changed with time \(t\), then the adiabatic evolution of time-dependent Schrodinger equation:

\[i\frac{d}{dt}|\psi(t)\rangle=H(\mathbf{R(t)})|\psi(t)\rangle\]

Take the Ansatz: \(|\psi(t)\rangle=e^{i\gamma_n(t)}e^{-i\int_0^tE_n(\mathbf{R(t')})dt'}|n(\mathbf{R(t)})\rangle\), we have

\[-\left(\frac{d}{dt}\gamma_n\right)|n\rangle+i\left|\frac{d}{dt}n\right\rangle=0\]

That gives the Berry phase expression:

\[\gamma_n(\mathcal{C})=\int_\mathcal{C}i\langle n(\mathbf{R})|\nabla_{\mathbf{R}}n(\mathbf{R})\rangle d\mathbf{R}\]

Define Berry connection:

\[\mathbf{A}^{(n)}(\mathbf{R})=i\langle n(\mathbf{R})|\nabla_{\mathbf{R}}n(\mathbf{R})\rangle=-Im\langle n(\mathbf{R})|\nabla_{\mathbf{R}}n(\mathbf{R})\rangle\]

Gauge transformation:

\[|n(\mathbf{R})\rangle \to e^{i\alpha(\mathbf{R})}|n(\mathbf{R})\rangle\]

\[\mathbf{A}^{(n)}(\mathbf{R}) \to \mathbf{A}^{(n)}(\mathbf{R})-\nabla_{\mathbf{R}}\alpha(\mathbf{R})\]

\(\gamma=\oint\mathbf{A}(\mathbf{R})d\mathbf{R}\) is gauge invariant.

Gauge and Parallel transportation: recalling the arbitrary phase

\[|n(\mathbf{R})\rangle \to e^{i\alpha(\mathbf{R})}|n(\mathbf{R})\rangle\]

why shouldn’t we choose one which makes

\[\frac{d}{dt}|n\rangle\equiv 0\]

from

\[-\left(\frac{d}{dt}\gamma_n\right)|n\rangle+i\left|\frac{d}{dt}n\right\rangle=0\]

then we have

\[\gamma_n=0\]

There is no Berry Phase in this frame, which is called inertial frame, the condition \(\frac{d}{dt}|n\rangle\equiv 0\) is called parallel transportation. All the information resorted to \(|n(\mathbf{R})\rangle\), similar to a transformation from active frame to passive frame.

Berry curvature¶

Define the Berry curvature:

\[\mathbf{B}(\mathbf{R})=\nabla_{\mathbf{R}}\times \mathbf{A}^{(n)}(\mathbf{R})\]

Using Stokes theorem, we have for the Berry Phase:

\[\gamma_n(\mathcal{C})=\int_\mathcal{S}\mathbf{B}^{(n)}(\mathbf{R})d\mathcal{S}\]

where \(\mathcal{S}\) is any surface whose boundary is the loop \(\mathcal{C}\).

Two useful formula:

\(B_j=\epsilon_{jkl}\partial_kA_l=-Im\epsilon_{jkl}\partial_k\langle n|\partial_ln\rangle=-Im\epsilon_{jkl}\langle\partial_kn|\partial_ln\rangle\), that is \(\mathbf{B}^{(n)}=-Im\sum\limits_{n'\neq n}\langle\nabla n|n'\rangle\times\langle n'|\nabla n\rangle\).

\(\mathbf{B}^{(n)}=-Im\sum\limits_{n'\neq n}\langle\nabla n|n'\rangle\times\langle n'|\nabla n\rangle\), to calculate \(\langle n'|\nabla n\rangle\), start from:

\[H(\mathbf{R})|n\rangle=E_n|n\rangle\]

\[\Rightarrow (\nabla H)|n\rangle+H|\nabla n\rangle=(\nabla E_n)|n\rangle+E_n|\nabla n\rangle\]

\[\Rightarrow \langle n'|\nabla H|n\rangle+\langle n'|H|\nabla n\rangle=E_n\langle n'|\nabla n\rangle\]

\[\Rightarrow \langle n'|\nabla n\rangle=\frac{\langle n'|\nabla H|n\rangle}{E_n-E_{n'}}\]

then we get:

\[\mathbf{B}^{(n)}=-Im\sum\limits_{n'\neq n}\langle\nabla n|n'\rangle\times\langle n'|\nabla n\rangle=-Im\sum\limits_{n'\neq n}\frac{\langle n|\nabla H|n'\rangle\times\langle n'|\nabla H|n\rangle}{(E_n-E_{n'})^2}\]

which is gauge invariant!

Berry curvature from perturbation theory¶

We can use time-independent perturbation theory to derive the changes of instant snapshot basis:

\[H(\mathbf{R})|n(\mathbf{R})\rangle=E_n(\mathbf{R})|n(\mathbf{R})\rangle\]

we have

\[|n(\mathbf{R+\Delta R})\rangle=|n(\mathbf{R})\rangle+\sum_{m\neq n}\frac{\langle m|H(\mathbf{R+\Delta R})-H(\mathbf{R})|n\rangle}{E_n-E_m}|m(\mathbf{R})\rangle\]

We see that \(\langle n|\Delta n(\mathbf{R})\rangle=0\), which means we have used parallel transport gauge, more general, we should add a arbitrary phase factor in the above equation for \(|n(\mathbf{R+\Delta R})\rangle\).

\[\nabla_{\mathbf{R}}|n\rangle=\sum_{m\neq n}\frac{\langle m|\nabla_{\mathbf{R}}H|n\rangle}{E_n-E_m}|m\rangle\]

From \(\mathbf{B}^{(n)}=-Im\sum\limits_{n'\neq n}\langle\nabla n|n'\rangle\times\langle n'|\nabla n\rangle\), we also get:

\[\mathbf{B}^{(n)}=-Im\sum_{n'\neq n}\frac{\langle n|\nabla H|n'\rangle\times\langle n'|\nabla H|n\rangle}{(E_n-E_{n'})^2}\]

Also notice:

\[\begin{split}\sum_n\mathbf{B}^{(n)}=&-Im\sum_n\sum_{n'\neq n}\frac{\langle n|\nabla H|n'\rangle\times\langle n'|\nabla H|n\rangle}{(E_n-E_{n'})^2}\\ =&-Im\sum_n\sum_{n'< n}\frac{\langle n|\nabla H|n'\rangle\times\langle n'|\nabla H|n\rangle+\langle n'|\nabla H|n\rangle\times\langle n|\nabla H|n'\rangle}{(E_n-E_{n'})^2}\\ =&0\end{split}\]

Which gives:

\[\sum_n\gamma_n(\mathcal{C})=\int_{\mathcal{S}}\sum_n\mathbf{B}^{(n)}(\mathbf{R})d\mathcal{S}=0\]

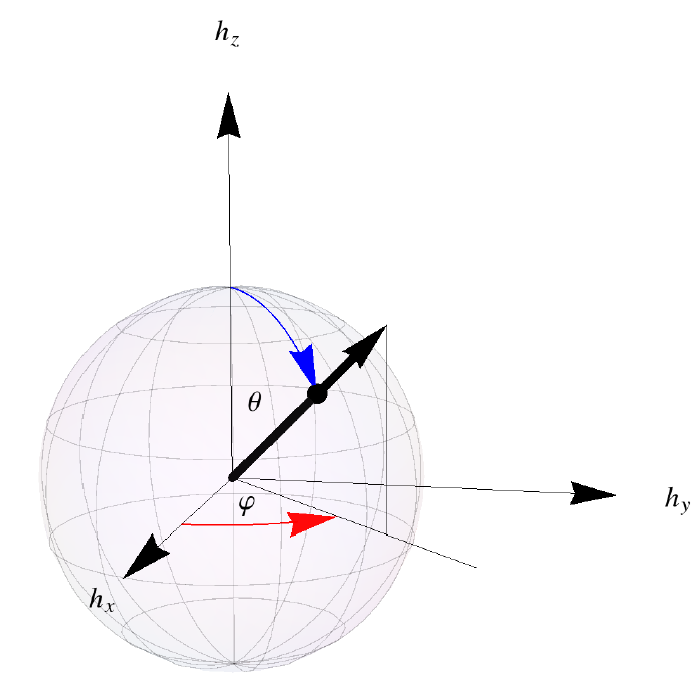
Benchmark: Spin-1/2¶

Gauge!Gauge!Gauge!

2-level Hamiltonian \(H(\mathbf{R})=h_0(\mathbf{R})\sigma_0+\mathbf{h}(\mathbf{R})\cdot\mathbf{\sigma}\), we can set \(h_0=0\), because it does not affect the eigenstates, eigen-energy are \(\pm|\mathbf{h}|\), introduce the unit vector:\(\hat{\mathbf{h}}=\mathbf{h}/|\mathbf{h}|\), the endpoints of \(\hat{\mathbf{h}}\) map out the surface of a unit sphere, called the Bloch sphere shows below:

Bloch sphere